1.Giriş
Lif takviyeli polimer kompozitlerin betonarme yapılardaki dolgu duvarlara uygulanmasını ve bu uygulamanın betonarme (BA) çerçeve sistem davranışına etkilerini daha önceki yazılarımızda kapsamlı olarak tartışmıştık.
Burada sunulan çalışmada, karbon esaslı lifli polimer kumaşların (CFRP) mevcut az katlı BA yapının dolgu duvarlarına uygulanmasının yapısal deprem davranışına katkısı kuramsal olarak irdelenmiştir. Kuramsal çalışmada deprem performansının belirlenmesi için doğrusal olmayan artımsal itme analizi yöntemi kullanılmıştır.
Betonarme yapı sistemi sergilediği deprem performansı açısından, yalın ve güçlendirilmiş dolgu duvarlı olmak üzere iki farklı durumda karşılaştırılmalı olarak değerlendirilmiştir. Önerilen güçlendirme yönteminin yapı performansına önemli katkılar sağladığı sonucuna varılmıştır.
Dolgu duvarlı betonarme çerçevelerin deneysel ve kuramsal olarak incelenmesi ile ilgili çalışmalar 1960’li yıllardan günümüze kadar devam etmiştir. Polyakov 1960 yıllarında yaptığı deneysel çalışmalar, dolgu duvarlı düzlem betonarme çerçevelerin davranışını anlamak açısından son derece önemli olmuştur.
Klinger ve Bertero (1976), Bertero ve Brokken (1983), Zarnic ve Tomazevic (1988), Mander ve Nair (1993)’in yapmış olduğu deneysel çalışmalar dolgu duvarlı betonarme çerçevelerin rijitlikleri ve dayanımlarının belirlenmesini sağlamıştır.
Dolgu duvarların çerçeve içerisinde uygun yerlerde kullanılması ile genel yapı dayanımının ve rijitliğinin artacağı bilinmektedir.
Dhanasekar and Page (1986), Mosalam (1996), Shing ve diğer (1994), dolgu duvarlı çerçevelerin yatay etkiler altındaki davranışını sonlu elemanlar yöntemi kullanarak modellemişlerdir. Sonlu elemanlar yönteminin bir dezavantajı da çok katlı yapıların çözümlenmesinde oldukça fazla zaman alması olarak belirtilebilir.
Bu tür yapılarda global davranışın bulunabileceği makro modeller kullanmak daha uygundur. Holmes (1961) dolgu duvarları, dolgu duvarların diyagonal uzunluğunun 1/3 genişliğin pandül çubuklar ile modellemiştir.
Stafford Smith (1962) ve Stafford Smith & Carter (1968) dolgu duvarları temsil ettiğini varsayan pandül çubukların genişliğini dolgu duvarlı çerçevenin yatay rijitlği parametresine bağlı olarak modellemiştir. Bu modele Mainstone (1971)’de rijitlik ilişkisine ampirik bağıntılar ile destek vermiştir.
Wood (1978) pencere açıklıkları bulunan dolgu duvarlı çerçevelerin göçme yükünü ve göçme modunun belirlenmesi için lineer olamayan lineer olmayan analizler gerçekleştirmiştir. Saneinejad ve Hobbs (1995) beton veya tuğla duvarlı çelik çerçevelerin yatay yükler altında hesap ve tasarımı için bir yöntem önermiştir.
Deneysel çalışmaların yanında lineer olmayan sonlu elamanlar yöntemiyle yapılan hesapların incelenmesi sonucunda, dolgu duvarların mekanik özelliklerinin bilinmesi halinde diyagonal çubuklarla modellenebileceği sonucuna varmıştır.
Negro ve Verzeletti (1996) 1/1 ölçekli gerçek bir yapı, PGA=0.3g yer ivmesi etkisinde benzeşik dinamik deney tekniği ile incelenmiştir.
Dolgu duvarların genel sistem davranışına olan etkisi enerjiler cinsinden açıklanmıştır. Tüm katlarda dolgu duvarlar bulunan çerçeve deneyinde yapıdaki yatay yer değiştirme ve dönmelerin diğer iki numuneye göre oldukça küçüldüğü belirtilmiştir.
Garevski ve diğer (2003) 1/3 ölçekli dolgu duvarlı ve CFRP ile güçlendirilmiş dolgu duvarlı numuneleri sarsma tablasında denemiştir. İzmit ivme kaydı PGA=0.023g’den PGA=0.45g’ye kadar artan genlikler etkisinde ardışık olarak test etmiştir.
Sarsma tablası deneylerinde PGA=0.45g en büyük ivme seviyesinde, yalın dolgu duvarlı numunede oluşan en büyük yatay tepe yer değiştirmesi 168 mm iken CFRP ile güçlendirilmiş numunede bu değer 87 mm’ye inmiştir.
Sofronie (2004), yığma duvarların kendi içsel sürtünmesi ile yapısal enerji tüketimine olan katkısını “yığma duvarlar polimer malzemeler ile güçlendirilirse sismik hareket sırasında tamamen aktif sönümleyici görevini üstlenirler” ifadesiyle belirtmiştir.
Dolgu duvarların çerçeve kolon ve kirişleri arasındaki yüzeyleri boyunca ve dolgu duvar üzerindeki derzleri boyunca oluşan sürtünmeler yapıya ilave sönüm sağlamaktadır. Bu sebeple dolgu duvarlar sistem dayanım ve rijitliğini artırmasının yanında, sönüm ve enerji tüketim kaynakları olarak da çalışmaktadır.
Yapısal sönüm artışı deprem isteminin azalmasına dolayısıyla etkiyen deprem yüklerinin küçülmesi anlamına gelmektedir. Priestly (2005) dolgu duvarlar tarafından tüketilen enerjinin önemini “dolgu duvarları olmadıkça, yapı sisteminde sürtünme kuvvetleri ihmal edilebilir düzeyde kalacaktır” ifadesiyle belirtmiştir.
Hashemi ve Mosallam (2006) ¾ ölçekli dolgu duvarlı betonarme çerçeveler üzerinde sarsma tablası deneyleri gerçekleştirmiştir. Çalışmada dolgu duvarların yapı rijitliğini 4 kat artırdığı, doğal titreşim periyodunu %50 oranında azalttığı, eş değer viskoz sönüm oranını %5-12 seviyelerine yükselttiği ve sönümlenen enerjiyi önemli oranda artırdığı belirtilmiştir.
Ozkaynak ve diğer (2016) dolgu duvarların yatayda tanımlanmış yay tipi elemanlar ile temsil edilebileceği “Duvar” isimli bir analitik model önermiştir.
Söz konusu modelde dolgu duvarlar; en büyük kayma dayanımı, başlangıç rijitliği, süneklik oranı ve diğer yapısal parametrelere bağlı olarak kurulan üç kırıklı kapasite eğrisi ile tanımlanmıştır. Çalışmada önerilen “Duvar” modeli yalın ve güçlendirilmiş duvarların, BA çerçeve davranışına katkısını temsil edebilme yeteneğine sahip olduğu belirtilmiştir.
Ozkaynak (2010)’ın tamamlamış olduğu geniş kapsamlı deneysel ve analitik çalışmalar, CFRP kumaşlar kullanılarak betonarme yapılardaki dolgu duvarların payandalı çaprazlı güçlendirme yöntemi ile güçlendirebileceğine ve bu uygulamanın yapı deprem performansına önemli katkılar sunacağına dikkat çekmektedir.
2. Analitik
Çalışma Burada sunulan çalışma kapsamında üç boyutlu betonarme yapı sisteminin lifli polimer kumaşlar ile güçlendirilmiş ve güçlendirilmemiş yalın durumdayken deprem davranışının belirlenmesi hedeflenmiştir. Bu amaçla her iki yapı lineer olmayan artımsal itme analizine tabi tutulmuştur.
Artımsal itme yönteminin kullanılabilmesi için; yapıda burulma düzensizliği olmaması, bina kat adedi bodrum kat hariç 8’i aşmaması ve hesaplanan hakim titreşim moduna ait etkin kütlenin toplam bina kütlesine oranının en az 0.70 olması gerekmektedir.
Artımsal eş değer deprem yükü yönteminde, hakim titreşim mod şekli ile orantılı olacak şekilde, deprem istem sınırına kadar tek doğrultuda adım adım artırılan eş değer deprem yüklerinin etkisinde doğrusal olmayan statik analiz yapılmaktadır.
Her bir hedef yer değiştirmeye karşılık gelen cevap dayanım ile aralarında kurulan ilişki kapasite eğrisi olarak tanımlanmaktadır. Kapasite eğrisi yapının genel olarak hangi deprem performansı seviyesinde olduğu hakkında önemli bilgiler vermektedir.
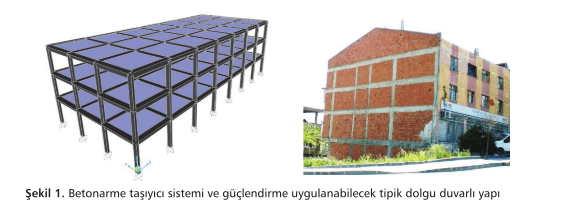
Çalışmada ele alınan BA yapının taşıyıcı sistemi Şekil 1’de verilmiştir. Bina taşıyıcı sistemi düzlem betonarme çerçevelerden oluşmaktadır. Uzun doğrultuda yerleşik tüm çerçevelerde kolonlar zayıf eksenleri etrafında eğilmektedir.
Binanın tüm katları 4.20 m yüksekliğinde olup, toplam yapı yüksekliği 12.6 metredir. İki ana doğrultuda kolon aksları arasındaki mesafeler 6 metredir.
Yapı yüksekliği boyunca kolon ve kiriş kesitleri sabit olup, iki tip kolon ve kiriş mevcuttur. Dış kolonlar 30×60 cm, iç kolonlar ise 30×70 cm kesit boyutlarına sahiptir. Dış kirişler 30×80 cm, iç kirişler ise 30×50 cm boyutlarındadır. Kolon elemanların boyutlarına bağlı olarak boyuna donatı oranları %1.0 ile %2.0 arasında değişmektedir.
Analitik modelin oluşturulmasında BA yapı sistemi çubuk elemanlar kullanılarak idealleştirilmiş ve analizler SAP2000 programında gerçekleştirilmiştir. Tüm analizlerde döşemelerin kendi düzlemlerinde sonsuz rijit davrandığı varsayılmıştır.
Betonarme kolon ve kiriş elemanların moment-eğrilik ilişkilerinin belirlenmesi için XTRACT yazılımı kullanılmıştır. Kesit plastik mafsal özellikleri dışarıdan ilgili noktalara atanmıştır. Betonarme elemanların mafsallar arasında kalan bölümleri için çatlamış eğilme rijitlikleri tanımlanmıştır.
Tablalı kirişlerin boyutları, kirişlerin açıklık ortasında ve mesnet bölgesinde olması durumlarına göre moment-eğrilik ilişkileri açısından birbirleri arasında farklılıklar göstermektedir.
Enine ve boyuna donatı kalitesi S220, gerçekleşen beton dayanımı 18 Mpa olarak belirlenmiştir. Enine donatı sıklaştırması mevcut olmadığı için betonda sargı etkisi dikkate alınmamıştır.
Betonarme yapının güçlendirilmesi için önerilen lifli polimer kumaşların kullanılma biçimi Şekil 2’de görülmektedir. Şekil 2’de görülmekte olan lifli polimer uygulaması, Ozkaynak (2010) çalışmasında ayrıntılı olarak incelenmiştir.
Betonarme yapının kat planı Şekil 3’te görülmektedir. Lifli polimer uygulaması ile güçlendirilmiş dolgu duvarların yer aldığı açıklıklar yapı kat planı üzerinde turuncu renkle gösterilmiştir.
Güçlendirilmiş yapıda güçlendirilmiş dolgu duvarların temsil edilmesi için Ozkaynak (2016) çalışmasında önerilen “Duvar” yay modeli kullanılmıştır. Söz konusu modelin oluşturulması için dışarıdan 5 adet giriş önemli bilgisine ihtiyaç duyulmaktadır.
Giriş bilgileri, Ozkaynak (2016) çalışması uyarınca boyutları bilinen dolgu duvar için en büyük kayma dayanımı (Vmak (Vcr= 50.4mm) ve dolgu duvarın düktilitesi (µ=8) olarak belirlenmiştir. Dolgu duvarın analitik modele dahil edilmesi ve çalışma prensibi şematik olarak Şekil 4’te gösterilmiştir.
Artımsal itme analizi FEMA440 kapsamında gerçekleştirilmiştir. FEMA440 gereğince, kapasite spektrumu yöntemi ile tanımlanan, spektral ivme ve spektral yer değiştirme eğrisi üzerinde performans noktasının belirlenmiş ve hedef performans noktaları esas alınarak yapının dolgu duvarların bulunmadığı ve bulunduğu durum için itme analizi gerçekleştirilmiştir.
Betonarme yapı 2.derece deprem bölgesinde ve Z1 türü zemin üzerinde bulunmaktadır. Deprem yönetmeliğinde (TDY-07) tanımlanan Z1 türü zemin için Ta=0.10 sn, Tb=0.30 sn olarak tanımlanmaktadır. Performans noktasının belirlenmesinde 50 yılda aşılma olasılığı %50 olan servis depremi kullanılacaktır.
Kolon, kiriş ve döşeme yükleri normal kat ve çatı katı için ayrı ayrı olarak hesaplanmıştır. İtme analizinde G+0.3Q düşey yükleri esas alınmıştır. Yapılan yük analizleri yapı genel boyutlarına göre değerlendirilip toplam yapı ağırlıkları, 1.ve 2. normal katlarda 9584.00 kN ve 3. katta ağırlığı ise 5670 kN olmak üzere toplam yapı ağırlığı 24840 kN olmuştur. Betonarme yapının analitik modeli üzerinde gerçekleştirilen serbest titreşim analizi sonucu, yapının birinci doğal titreşim peryodu 1.78 sn. olarak hesaplanmıştır.
Yukarıda belirtilen zemin özellikleri, depremsellik ve %5 viskoz sönüm dikkate alınarak belirlenen deprem istemi eğrisi, spektral formatta (Sa-Sd) kapasite eğrisi ile aynı ortamda bulundurularak konarak performans noktası hesaplanmıştır.
Elastik istem eğrisi ve kapasite eğrisi başlangıç rijitlikleri kesiştirilerek Sd yer değiştirmesi eşit yer değiştirme yaklaşımıyla inelastik davranışta ulaşılacak yer değiştirmeye karşı gelmektedir. Her iki doğrultuda yapılan hesap sonucu yalın durum için performans noktaları Sdx=0.38 ve Sdy=0.26 olarak belirlenmiştir.
Fiziksel yer değiştirme karşılıkları da δx=490 mm ve δy=343 mm’dir. Güçlendirilmiş durumda ise deprem istem eğrisi olarak, %10 sönüm oranı için belirlenen spektral eğri esas alınmıştır.
Performans noktaları güçlendirilmiş durumda Sdx=0.06, Sdy=0.08 ve karşılık gelen fiziksel yer değiştirmeler δx=70 mm ve δy=100 mm olarak hesaplanmıştır. Güçlendirilmiş durumda yer değiştirme istemi uzun doğrultuda 7 kat kısa doğrultuda 3 kat azalmıştır.
Yalın Durum, Güçlendirilmiş Durum
Yalın ve güçlendirilmiş durumda aynı çerçeveler karşılaştırıldığında plastik mafsal dağılımları incelenmiş ve renklendirilmiş hasar dağılımları Şekil 6’da verilmiştir. Güçlendirilmiş sistemde birçok kesitte plastik mafsal oluşmadığı ve oluşan plastik mafsalların ise hemen kullanım (IO) performans seviyesi civarında kaldığı görülmektedir.
3. Sonuçlar
1. Üç boyutlu yapı sisteminde iki doğrultuda yeterli sayıda dolgu duvarı CFRP ile sargılanarak mevcut deprem güvenliği artırılmıştır. Göreli kat ötelenmeleri, kolon ve kiriş uç plastik dönmeleri FEMA 356 ya göre değerlendirilerek yapının performans düzeyinin iyileştiği görülmüştür.
2. Mevcut yapıda önerilen güçlendirme yöntemiyle yerdeğiştirme uzun ve kısa doğrultuda sırasıyla 7 kat ve 3 kat azalma sağlanmıştır. Kapasite eğrileri, güçlendirilmiş durum için uzun doğrultuda yaklaşık 5 kat dayanım artışının; kısa doğrultuda ise 4 kat dayanım artışının sağlandığını göstermiştir.
3. Güçlendirilmiş durumda yapının uzun doğrultusu için performansı, göçmenin önlenmesi (GÖ) performans seviyesinden hemen kullanım (HK) performans seviyesine iyileşmiştir. Güçlendirilmiş durumda birçok kesitte plastik mafsal oluşmadığı gözlenmiştir.
Doç. Dr. Hasan Özkaynak / Beykent Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü
4. Referanslar
[1] Bertero V. and Brokken S. (1983) “Infills in Seismic Resistant Building” Journal of Structural Engineering Vol. 109, Issue 6. [2] Dhanasekar, M. and Page, A.W. (1986). “The Influence of Brick Masonry Infill Properties on The Behaviour of Infilled Frames”. Proc Inst of Civil Engrs,London. pp 593–605 [3] FEMA-356. 2000. Prestandard and Commentary for the Seismic Rehabilitation of Buildings. Prepared by ASCE Reston, Virginia Prepared for Federal Emergency Management Agency Washington, D.C. 273 [4] FEMA-440 2005. Improvement of Nonlinear Static Seismic Analysis Procedures, prepared by ATC forAmerican Society of Civil Engineers for Federal Emergency, Washington, D.C. [5] Garevski, M., Paskalov, A., Talaganov, K. and Hristovski, V., 2003. Experimental and Analytical Investigation of 1/3-Model R/C Frame- Wall Building Structures – PART I(Model Design and Analytical Evaluation of Dynamic Characteristics of the Model). NATO SfP 977231 Project: “Seismic Assessment and Rehabilitation of Existing Buildings”, NATO Science Series, IV. Earth and Environmental Sciences-Vol.29, pp.487-498. [6] Hashemi, A. and Mosalam, K.M., 2006. ShakeTable Experiment on Reinforced Concrete Structure Containing Masonry Infill Wall. Earthquake Engineering and Structural Dynamics. Vol.35, no.14, pp.1827-1852. [7] H. Özkaynak, M. Sürmeli, E. Yüksel “A capacity curve model for confined clay brick infills”, Bulletin of Earthquake Engineering, March 2016, Volume 14, Issue 3, pp 889-918 [8] Hasan ÖZKAYNAK, Temmuz 2010: “Dolgu Duvarları Lifli Polimerler ile Sargılanmış Betonarme Çerçeve Sistemlerin Deprem Davranışı ve Yapısal Sönüm Özellikleri” Doktora Tezi, İstanbul Teknik Üniversitesi, Fen Bilimleri Enstitüsü, İnşaat Mühendisliği Anabilim Dalı,Deprem Mühendisliği Programı, Tez Danışmanı: Prof. Dr. Ercan YÜKSEL [9] Holmes, M., 1961. Steel Frames With Brickwork And Concrete Infilling.Proceedings of the Institute of Civil Endineers, London, England, Part 2, Vol. 19, pp.473-478. [10] Klinger, R.E. & Bertero, V.V. (1976). Infilled frames in earthquake resistant construction. Earthquake Engineering Research Center, University of California, Berkeley, CA, Rep. EERC 76-32, Dec [11] Mainstone, R. J. (1971). On the stiffness and strengths of infilled frames, Proceedings, Institution of Civil Engineers, Supplement IV, 57–90 [12] Mander J.B. and Nair B., 1993 “Seismic Resistance of Brick-Infilled Steel Frames with and without Retrofit” The Masonry Society Journal 12(2):24-37. [13] Mosalam KM, 1996. Experimental and Computational Strategies for the Seismic Behavior Evaluation of Frames with Infilled Walls. PhD Thesis Cornell Univesity, Ithaca, NY, 1996. [14] Negro, P. and Verzeletti, G., 1996. Effect of Infill on the Gloabal Behaviour of R/C Frames: Energy Considerations from Pseudodynamic Tests. Earthquake Engineering and Structural Dynamics. Vol.25, pp.753-773. [15] Priestly M.J.N. and D.N.Grant., 2005. Viscous damping in seismic design and analysis. Journal of Earthquake Engineering. Vol.9, Special Issue 2, pp.229-255. [16] SAP2000v12, Structural Analysis Program, Computer and Structures Inc., Berkeley, California. [17] Shing, P.B., Bursi, O.S., Vannan, M.T., 1994. Pseudodynamic Tests of Concentrically Braced Frame Using Substructuring Techniques. Journal of Constructional Steel Research, vol.29, pp.121-148. [18] Shing P.B, Mehrabi, A.B., Schuller, M and Noland, J.D., 1994 “Experimental evaluation and finite element analysis of masonry-infilled R/C frames”
Proc.of the Eleventh Conference held in conjuction with ASCE Structures Congress’94 and Internatitonal Symposium’94, Atlanta, Georgia, pp.84-93. [19] Smith,B.,S., 1962. Lateral Stiffness of Infilled Frames. Journal of the Structural Division. Proceedings of the American Society of Civil Engineers, Vol. 88, no. 183. [20] Stafford-Smith B.S. (1968). Model Test Results of Vertical and Horizontal Loading of Infilled Frames, ACI Journal, Volume 65, No. 8: 618-625 [21] Saneinejad, A. & Hobbs, B., 1995. Inelastic Design of Infilled Frames. Journal Structural Engineering, ASCE, Vol. 121, No.4, pp.634-650. [22] Sofronie, R. 2004. Performances in Seismic Strengthening of Masonry. 13th
World conference on earthquake engineering Vancouver; Canada, BC.Paper no. 182. [23]TDY, 2007. Deprem Bölgelerinde Yapılacak Binalar Hakkında Yönetmelik. Bayındırlık ve İskan Bakanlığı, Ankara. [24] TS 500, 2000. Betonarme Yapıların Tasarım ve Kuralları, Türk Standartları Enstitüsü, Ankara. [25]TS 498 1987. Yapı Elemanlarının Boyutlandırılmasında Alınacak Yüklerin Hesap Değerleri, Türk Standartları Enstitüsü, Ankara. [26] Wood R.H. (1978) “Plasticity, composite action and collapse design of unreinforced shear wall panels in frames” Proceedings of Institute of Civil Engineers, Part 2, 65 June 381-411. [27] XTRACT V3.0.7., 2006. Cross-sectional Structural Analysis of Components. Imbsen Software Systems, Sacramento, CA. [28] Zarnic R, Tomazevic M (1988) An experimentally obtained method for evaluation of the behavior of masonry infilled RC frames. In: 9th on earthquake engineering, pp 163–168 world conference
